IMPORTANCIA DE ESTIMAR EL TAMAÑO MUESTRAL

La estimación del número de unidades experimentales (sujetos, animales, células…) requeridas para responder a una pregunta experimental es un paso importante en la fase de planificación del estudio. No se trata de una decisión trivial, si no que el cálculo adecuado del tamaño muestral nos permitirá obtener resultados concluyentes y reproducibles o por el contrario los resultados no serán informativos ni robustos.

¿Por qué es importante?
Porque precisamente el número de unidades experimentales que necesito en cada grupo es lo que determinará la probabilidad de demostrar que el tratamiento/intervención es efectiva. Y si no se puede demostrar, se habrá realizado un uso no ético de animales en experimentación.

¿Qué es necesario para calcular el tamaño muestral? ¿La experiencia? No. Como todo: una buena planificación. El número de sujetos/animales no se puede decidir de manera arbitraria, no es ético, ¿y por qué? Pues porque se pueden dar estos dos supuestos:

• La situación A: donde se utiliza un número insuficiente de animales, por lo que no se obtienen resultados concluyentes. Por tanto, se ha realizado un uso de animales en investigación sin llegar a concluir nada debido a la falta de potencia, y se ha desperdiciado dinero y tiempo (equivale a más dinero). Conclusión: no es ético.

• La situación B: donde se utiliza un número excesivo de animales, pudiendo demostrar la misma conclusión con menor cantidad. De modo que se realiza igualmente un uso de animales innecesario, dinero y tiempo (más dinero). Conclusión: no es ético.

Conclusión: es obligatorio plantearnos y planificar el tamaño de la muestra. ¿Por dónde empiezo? Por responder las siguientes preguntas:

¿Qué sería un resultado relevante en mi experimento? ¿Qué estoy buscando?

Estas son las preguntas que nos hacemos cuando queremos decidir a priori el TAMAÑO DE EFECTO que consideramos sería relevante en el experimento. Por ejemplo, se está probando un tratamiento que disminuye la presión arterial sistólica en individuos con hipertensión. Como existe mucha información al respecto y bibliografía, sabemos que la media aproximada en este grupo de individuos es de 160. ¿Qué esperaría del tratamiento? ¿Qué sería un resultado interesante? ¿Una disminución de 0,05 en la media de 160 sería un resultado interesante? ¡En absoluto, menuda birria de disminución! ¿Y una disminución de 7 unidades? Bueno, ¡eso sí! Estas son las preguntas que debemos hacernos.

En la mayoría de ocasiones, la investigación en cuestión, no se ha realizado nunca porque es una técnica novedosa o básicamente porque si no fuese una investigación pionera, no habría nada que publicar. Sin embargo, esto no significa que no podamos dar una cifra estimada de lo que esperamos, y si no es así, entonces lo mejor es empezar por un estudio piloto para estimar la media y variabilidad de dicha variable de interés en este contexto concreto.

¿Qué tipo de fluctuaciones espero alrededor de la media de mi parámetro de interés?

Esto se refiere a la VARIABILIDAD de los datos. Bien, ¿y cómo puedo saber la variabilidad o dispersión que espero? Es una técnica novedosa, ¡no existe nada publicado al respecto! De acuerdo, pero sabiendo que nuestra media es de 160, con mi experiencia y conocimiento seré capaz de decidir si es más probable que obtenga datos de la muestra con más variabilidad (154.10, 157.90, 160.80, 164.78) o menos (159.84, 160.12, 160.54, 158.99). Esto es importante, porque evidentemente será más fácil detectar diferencias en una medida que es más precisa y menos variable que en otra que tiene un mayor rango de los datos (están más dispersos, mayor variabilidad).

Con esta información podemos determinar aproximadamente la variabilidad, y lo mejor es que seamos conservadores si no podemos cuantificar exactamente la varianza. Para ello, podemos aumentar un 10 o 20% la desviación y así aseguramos que los datos que se puedan obtener estén contenidos en el rango esperado.

Lo ideal es que pudiésemos reportar información acerca de la variabilidad del grupo control y del grupo tratamiento. No obstante, si el tratamiento es novedoso, lo lógico es que no podamos dar una estimación de la variabilidad. En ese caso, asumiremos que la varianza del grupo tratamiento es tan grande como la del grupo control.

¿Qué porcentaje de falsos positivos estoy dispuesto a asumir?

Sabemos que cuando contrastamos una hipótesis, existe la posibilidad de que el test determine que existe una diferencia entre el grupo tratamiento y control cuando en realidad, no existe tal diferencia. Esto es lo que se conoce como un falso positivo o la probabilidad de error de tipo I. Si elegimos el estándar 0.05, entonces el NIVEL DE CONFIANZA será del 95%. Es decir, asumimos que el 5% de las veces concluiremos erróneamente que los grupos son distintos.

¿Qué potencia quiero tener?

Es decir, ¿Qué SENSIBILIDAD espero que tenga mi muestra para detectar diferencias cuando realmente existen? La potencia se calcula como 1 – β (también conocido como error de tipo II). La probabilidad de error de tipo II determina el porcentaje de veces que asumimos que, habiendo una diferencia entre los grupos, no seremos capaces de detectarla y por tanto estaremos cometiendo un falso negativo. Normalmente asumimos un error de tipo II de 20%, pero si nosotros queremos realmente ser más sensibles, deberemos fijar una mayor potencia. Esto se traducirá en un mayor número de animales.

Las dos primeras preguntas se refieren a la recopilación de información previa. Y este es un paso obligatorio, no podemos decir que esperamos un efecto estandarizado de 0.7 simplemente porque nos cuadra el número de animales, no. El efecto estandarizado lo debemos obtener a partir de la variabilidad esperada y el efecto que consideraríamos relevante. Y las dos últimas cuestiones se refieren a la probabilidad de cometer falsos positivos y falsos negativos que estoy dispuesto a asumir. Aunque habitualmente la probabilidad de error de tipo I se ha establecido en 0.05 y la probabilidad de error de tipo II en 0.2, nosotros podemos justificar la necesidad de utilizar otro límite.

Uso de GPower

Los cálculos reales pueden ser un poco engorrosos, por eso existen multitud de calculadoras online, hojas de cálculo y software (más y menos complejos) para la estimación del tamaño muestral. Desde la Oficina de Investigación Responsable recomendamos el programa GPower desarrollado en la Universidad de Düsseldorf.
Se trata de un software gratuito de cálculo del poder estadístico. Se ha desarrollado tanto para Windows como para Mac OS X y se puede descargar en el siguiente enlace:

Enlace de descarga de GPower

También se puede descargar el manual de uso. Existe una versión corta tipo tutorial y un manual más completo: Tutorial versión reducida y Manual versión extendida .
También añadimos el enlace al artículo Power, effect and sample size using GPower: practical issues for researchers and members of research ethics committees. Este documento sirve de apoyo en cuanto a los conceptos relativos al tamaño de efecto de los diferentes tipos de test, y su efecto en el tamaño muestral.
A continuación, presentamos una breve demostración del cálculo muestral para una diferencia de medias y para una diferencia de proporciones. Lo primero que debemos determinar en la estimación de la muestra es la variable de interés o variable respuesta o primary outcome (existen muchas maneras de denominarla). Esta es una decisión muy importante, porque el tipo de variable influirá de manera considerable en el tamaño de la muestra: una variable continua siempre tendrá más sensibilidad que una variable categórica, por lo que siempre que sea posible, se recomienda medir en continuo la respuesta, así el tamaño muestral requerido será menor.

En el caso de una diferencia de medias, la variable de interés es una variable numérica continua; mientras que en el caso de diferencia de proporciones, la variable respuesta se trata de una variable dicotómica (si/no, vivo/muerto, éxito/fracaso). Se dice que es una proporción porque se analiza el resultado global de la muestra que es la fracción del número de casos positivos/favorables/de interés entre el número de casos totales. Por ejemplo: si analizamos supervivencia a los 5 años en 100 individuos, y tras el período de seguimiento han fallecido 10 personas, la proporción de supervivencia a los 5 años es del 90% o 0,9.

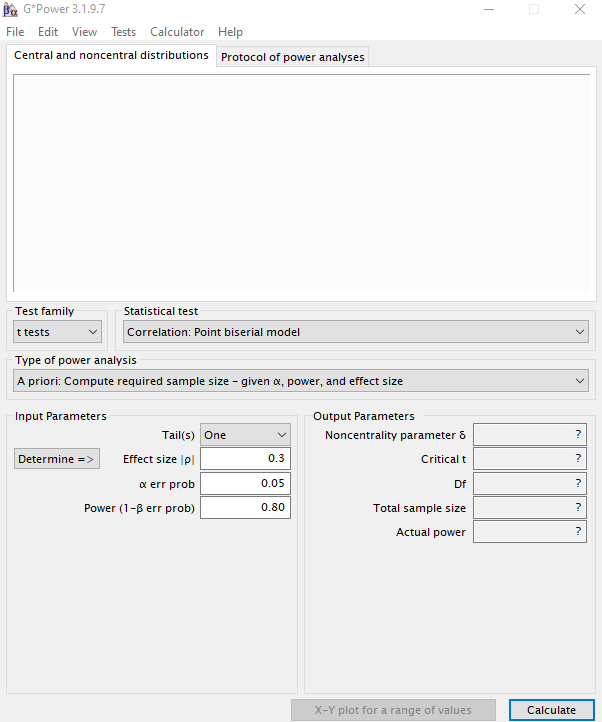
Esta es la pantalla principal que se muestra cuando se inicia GPower. Para el cálculo de cualquier tamaño muestral, debemos determinar:

1. 1. El Test family adecuado a nuestro experimento. Esta es la cuestión más técnica dado que debemos pensar en la distribución del estadístico del test que se realizará al final en el análisis de los resultados. Por ejemplo, si sabemos que vamos a comparar la media del grupo control con la del grupo tratamiento, haremos la comparación mediante el test t de Student. Sin embargo, si vamos a realizar un ANOVA, entonces el estadístico del test sigue una distribución F de Snedecor. No es necesario estar familiarizado con el Test family, porque en función de la opción que se seleccione, veremos aparecer el test que queremos realizar en el apartado Statistical test.
   2. Statistical test. En esta pestaña se muestra una lista de situaciones experimentales de acuerdo a la pestaña Test family, de entre las cuáles debemos seleccionar la que se ajuste a nuestro experimento.
   3. Type of power analysis muestra 5 tipos de estimación de la potencia. El más utilizado es el análisis a priori, porque es el que necesitamos hacer en la planificación del estudio. En este tipo de análisis se calcula la N requerida dadas nuestras asunciones: efecto, variabilidad, error de tipo I y error de tipo II.

Estimación del tamaño muestral para una diferencia de medias

En esta demostración, vamos a calcular el número de individuos necesarios para estudiar la efectividad de un nuevo tratamiento desarrollado para reducir la hipertensión. Para demostrar nuestra hipótesis, consideraremos la variable cuantitativa tensión arterial sistólica como nuestra variable respuesta. Dado que se trata de una variable numérica continua, la analizaremos en la fase de resultados con un test t (en principio). Por tanto, en Test Family seleccionamos “t tests”.

El primer parámetro que debemos determinar es la unilateralidad o bilateralidad del contraste. Por regla general se recomiendan contrastes bilaterales, porque el contraste unilateral solamente detectaría efectos que disminuyesen la media del grupo control. Sin embargo, en biología muchas veces no conocemos la dirección del efecto que se va a observar. Por tanto, seleccionamos bilateral: Tails = Two.

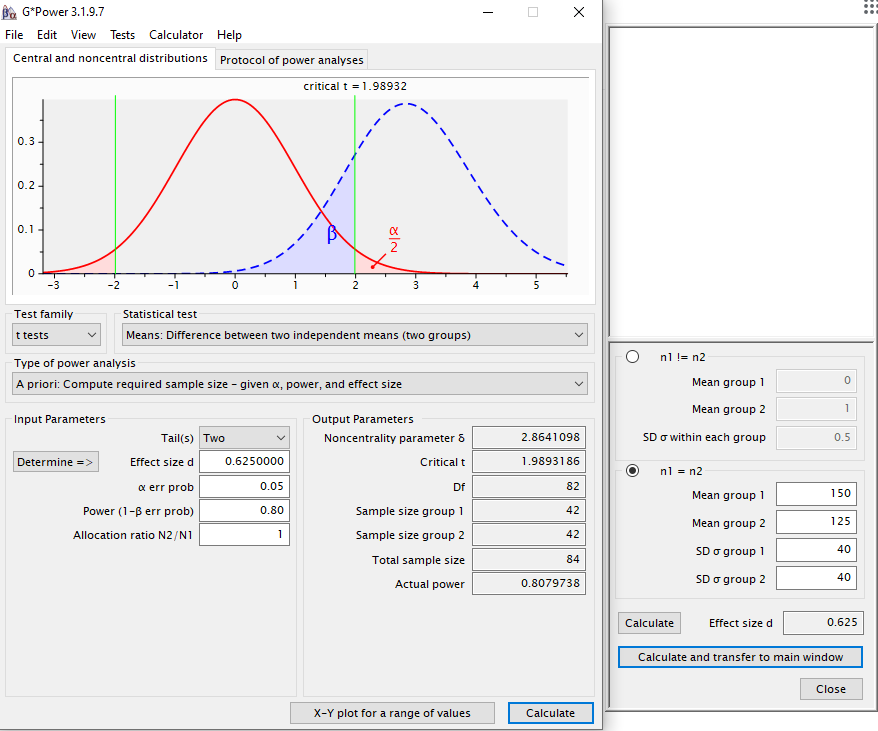
En segundo lugar determinamos el tamaño del efecto d. Este parámetro está normalizado, así que para introducir nuestra información a priori, clicamos en el botón Determine => y aparecerá la pantalla que se muestra en la parte derecha. Decidimos que los dos grupos tengan el mismo tamaño y nos paramos un momento a pensar en los parámetros: el diseño del experimento consiste en dos grupos: control y tratamiento, este último tomará el nuevo fármaco mientras que al grupo control se le administrará placebo. Con nuestra experiencia, sabemos que en este perfil patológico el nivel promedio de tensión arterial sistólica es 150, por tanto, asumiremos que el grupo control tendrá dicha media. En cuanto al tamaño del efecto, o lo que es lo mismo, la diferencia esperada en relación al grupo tratamiento no la sabemos, porque es el primer ensayo de este tratamiento. De todos modos, vamos a determinar que la media del grupo tratamiento es 125. Esto no significa que realizaré el experimento y efectivamente obtendré este resultado, pero si es así, si disminuye en 25 unidades, seré capaz de detectarlo con este número de individuos, la potencia fijada y el nivel de confianza determinado. Es decir, quiero detectar si la tensión sistólica disminuye en 25 unidades y se estabiliza en una cifra que consideraríamos normal, sin problemas patológicos.

Después debemos fijar la variabilidad de los grupos. En el grupo control sabemos por multitud de artículos que la desviación estándar de esta variable está alrededor de 40. Sin embargo, del grupo tratamiento no tenemos ningún dato, por lo que asumiremos que es igual de grande (estamos siendo conservadores, pues al esperar una media menor, podría tener una SD menor). Así que fijamos 40 de SD en ambos grupos y clicamos en calcular tamaño del efecto y transferir a la pantalla principal.

El efecto estandarizado obtenido es de 0.625, es decir queremos detectar 0.625 desviaciones estándar del grupo control. A continuación, especificamos la probabilidad de error de Tipo I o α, es decir, qué porcentaje de veces estamos dispuestos a equivocarnos diciendo que el fármaco tiene un efecto cuando en realidad no lo tiene, por defecto dejamos 0,05. En cuanto a la potencia, salvo casos debidamente justificados, especificamos una potencia del 80% (0,8). Y por último dejamos la Allocation ratio = 1 para que ambos grupos tengan el mismo tamaño. Clicamos en el botón Calculate y obtenemos que cada grupo debe estar formado por 42 individuos, en total 84.

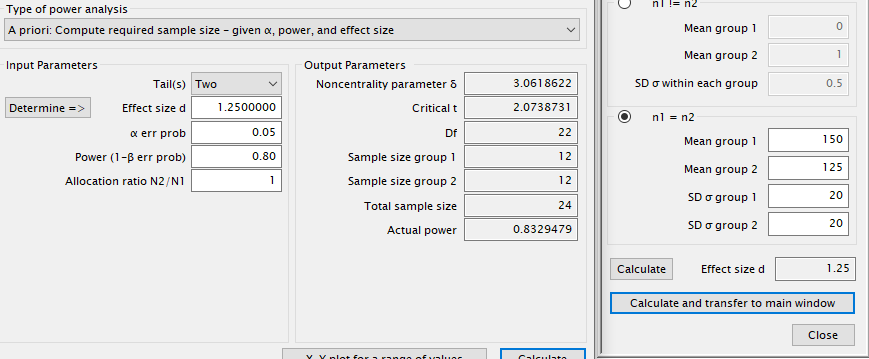
Podemos ver el efecto que tiene la variabilidad sobre el tamaño muestral en la siguiente figura. Hemos modificado el parámetro SD, disminuyendo la desviación estándar de 40 a 20 en ambos grupos y manteniendo el resto de parámetros constantes. El resultado de esta estimación sería de 12 individuos por grupo. Es decir, con un total de 24 individuos seríamos capaces de detectar una disminución de 25 unidades dada una SD de 20 uds, un nivel de confianza del 95% y una potencia del 80%. Conclusión: menor variabilidad, menor número de sujetos requerido.

Estimación del tamaño muestral para una diferencia de proporciones

Este segundo experimento es muy similar al anterior, excepto por la variable respuesta. Vamos a probar el mismo tratamiento con el mismo diseño experimental, pero en vez de medir la efectividad del tratamiento como el número de unidades que disminuye la tensión arterial sistólica, ahora vamos a medirlo como la proporción de individuos hipertensos en un grupo y en otro.
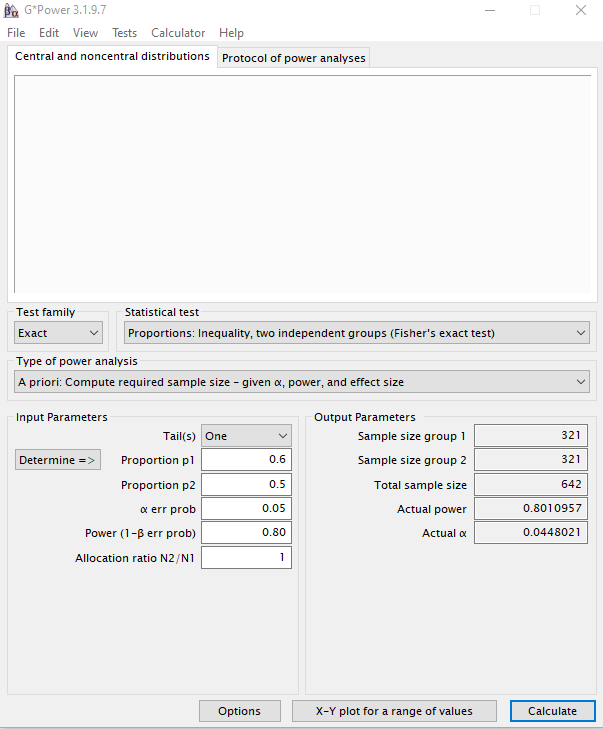
En este caso, dado que queremos comparar dos proporciones de dos grupos independientes seleccionamos en Test family: Exact y en Statistical test: Proportions: Inequality, two independent groups (Fisher’s exact test). Mantenemos seleccionado en el tipo de análisis de la potencia: A priori.

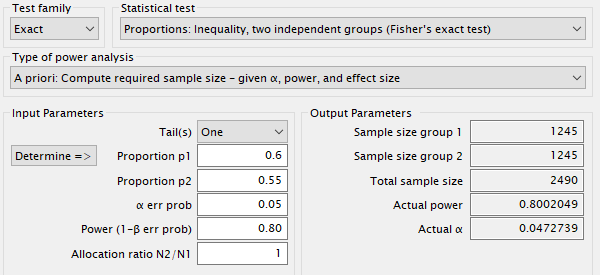
Solamente queremos detectar si la proporción de personas hipertensas en el grupo tratamiento es inferior al grupo control, por lo que seleccionamos el contraste One tail (unilateral). Los contrastes unilaterales requieren tamaños muestrales inferiores a los contrastes bilaterales. En segundo lugar, determinamos el porcentaje de individuos hipertensos en este tipo de población envejecida que estamos estudiando: por bibliografía determinamos esta proporción en 0,6 (60%). A continuación, fijamos la proporción del grupo tratamiento en 0,5. Esto significa que queremos ser capaces de detectar esta diferencia de proporciones si el nuevo fármaco es capaz de reducir en un 10% la proporción de individuos hipertensos. No significa que vaya a ser así, pero si lo fuese, seríamos capaces de detectarlo con un nivel de confianza del 95% y una potencia fijada del 80%.

Calculamos el tamaño muestral para determinados parámetros, y obtenemos un tamaño muestral de 642 individuos (321 en el grupo control y 321 en el grupo tratamiento). Si en vez de esperar un 10% de diferencia en la proporción de hipertenso entre ambos grupos, somos menos optimistas, y esperamos solamente un cambio del 5%, necesitaríamos una muestra total de 2490 individuos (1245 en cada uno de los grupos) para poder detectar la efectividad del tratamiento. Conclusión: 1) un menor efecto esperado, conlleva un mayor tamaño muestral. 2) un contraste de proporciones siempre tendrá menor potencia y requerirá un mayor tamaño muestral. Por tanto, sustituir siempre que sea posible las variable categóricas por variables cuantitativas.